На стороне AB треугольника ABC отметили точку M так, что AM=BC. Из точек M и B на сторону AC опустили перпендикуляры MK и BH (см. рис.). AC вдвое больше KH. Угол A равен 22 градусам. Найдите угол C.

(задача Максима Волчкевича с сегодняшнего Матпраздника — доступна начинающим)

Via @don_schijuan

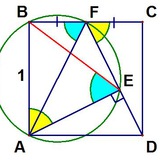
Центры вписанных коник изогонально сопряжены => точки касания лежат на 1 окружности

Друзья! Напоминаю, что сейчас и до конца марта идёт первый турнир нового сезона Квантландия с интерактивными задачами и головоломками. В этот раз мы сделали отдельно Турниры для 4-6 класса и для 7-9 класса, но участвовать могут и взрослые. Участие бесплатное, достаточно зарегистрироваться на сайте турнира https://math.kvantland.com/ и приступить к задачам (можно возвращаться к задачам в другой день и брать подсказки). Важно: лучше использовать ноутбук (не смартфон) и при регистрации на турнир на сайте использовать не gmail-почту, а альтернативную (yandex, mail,…), так как на gmail часто не приходит подтверждение регистрации. По итогам сезона мы наградим победителей!

Ну а сегодня задача по геометрии из предыдущего турнира для 7-9 класса:
На гипотенузе AB прямоугольного треугольника ABC отмечена точка D, из которой опущен перпендикуляр DE на катет BC. Найдите угол BCD, если AC = CD + DE, а угол CAE равен 23°.
Подписаться на Телеграм-канал
#Новости #ГеометрияДляВсех

В пространстве дан трехосный эллипсоид. Найти геометрическое место точек, из которых его контур виден, как круг. Иначе говоря, найти геометрическое место вершин круговых конусов, описанных около данного эллипсоида.

Квантик нарисовал выпуклый многоугольник и легко заштриховал его, проводя отрезки с концами на сторонах многоугольника.

Потом он подумал – а можно ли заштриховать любой выпуклый многогранник (вместе с внутренностью), проводя отрезки с концами на его рёбрах? Или для каких-то многогранников это не удастся и внутри останутся незаштрихованные пустоты?

// коллега Дориченко рассказал задачку

а) Стороны треугольника T2 на 1 больше соответствующих сторон треугольника Т1. Обязательно ли треугольник Т1 можно накрыть треугольником Т2?

б) Даны два тетраэдра; каждое ребро второго тетраэдра длиннее соответствующего ребра первого ровно на метр. Обязательно ли внутри второго тетраэдра можно разместить тетраэдр, равный первому? (Точкам нового тетраэдра разрешено попадать на границу второго.)

// А.Акопян по мотивам Р.Шварца; via https://www.tg-me.com/matheduks/207

Почему-то люблю эту задачу. Дан треугольник ABC. Окружность w касается сторон AB и AC и (ABC). Биссектриса угла ABC пересекает AC и (ABC) в точках X и Y. Докажите, что (AXY) касается w.

еще одна теорема о замыкании: если кругов четное количество, то цепочка на картинке замыкается за один круг (а если нечетное — за два круга)

// из https://arxiv.org/abs/2502.15751 via Д.А.Терешин

Еще одна задачка про красную окружность. Дан треугольник ABC с вписанной окружностью w. Биссектриса угла ABC пересекает AC и (ABC) в точках X и Y. Касательная параллельная BC к w пересекает (AXY) в точке T. Докажите, что YT касается w.

(СПБ-МО 2025 10.2)
Дан угол с вершиной A, величина которого меньше 180, и
число s > 0. На сторонах угла выбирают точки B и C так, что
площадь треугольника ABC равна s. Докажите, что существуют
такие точки X и Y (не зависящие от выбора точек B и C), что
точки B, C, X, Y всегда лежат на одной окружности.